


#PERMUTATIONS FREE#
txt file is free by clicking on the export iconĬite as source (bibliography): Permutations on dCode. Before we discuss permutations we are going to have a look at what the words combination means and permutation. For example, if you have a lock where you need to.
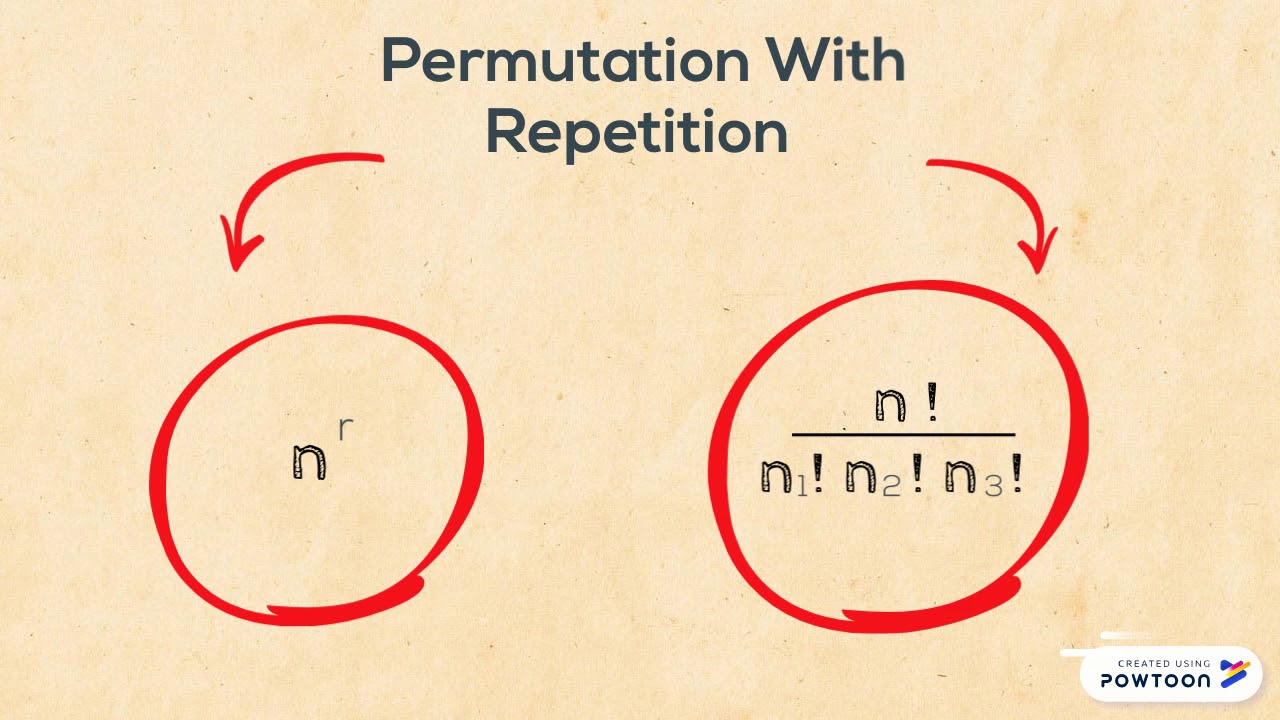

In some scenarios, the order of outcomes matters. For example, with four-digit PINs, each digit can range from 0 to 9, giving us 10 possibilities for. To calculate the number of permutations, take the number of possibilities for each event and then multiply that number by itself X times, where X equals the number of events in the sequence.
#PERMUTATIONS HOW TO#
And then you’ll learn how to calculate the total number of each. Analysts also call this permutations with replacement. Let’s understand this difference between permutation vs combination in greater detail. The copy-paste of the page "Permutations" or any of its results, is allowed (even for commercial purposes) as long as you cite dCode!Įxporting results as a. Permutations: The order of outcomes matters.
#PERMUTATIONS ANDROID#
Except explicit open source licence (indicated Creative Commons / free), the "Permutations" algorithm, the applet or snippet (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or the "Permutations" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) and all data download, script, or API access for "Permutations" are not public, same for offline use on PC, mobile, tablet, iPhone or Android app! Ask a new question Source codeĭCode retains ownership of the "Permutations" source code. Five are needed to clean windows, two to clean carpets and one to clean the rest of the house.Example: DCODE 5 letters have $ 5! = 120 $ permutations but contain the letter D twice (these $ 2 $ letters D have $ 2! $ permutations), so divide the total number of permutations $ 5! $ by $ 2! $: $ 5!/2!=60 $ distinct permutations. In how many different ways can the students be assigned to these rooms? (one student will sleep in the car)ġ1) Eight workers are cleaning a large house. In how many ways can he distribute the cones among the children.ġ0) When seven students take a trip, they find a hotel with three rooms available - a room for one person, a room for two poeple and a room for three people. In mathematics, permutation is a technique that determines the number of possible ways in which elements of a set can be arranged. Note that ABC and CBA are not same as the order of arrangement is different. For example: The different ways in which the alphabets A, B and C can be grouped together, taken all at a time, are ABC, ACB, BCA, CBA, CAB, BAC. Ways to assign the workers to these tasks.įind the number of distinguishable permutations of the given letters.ĥ) In how many ways can two blue marbles and four red marbles be arranged in a row?Ħ) In how many ways can five red balls, two white balls, and seven yellow balls be arranged in a row?ħ) In how many different ways can four pennies, three nickels, two dimes and three quarters be arranged in a row?Ĩ) In how many ways can the letters of the word ELEEMOSYNARY be arranged?ĩ) A man bought three vanilla ice-cream cones, two chocolate cones, four strawberry cones and five butterscotch cones for 14 children. Permutations are the different ways in which a collection of items can be arranged.


 0 kommentar(er)
0 kommentar(er)
